The Schrödinger Equation

Posted on 28/07/2023

The Schrödinger equation was formulated by Erwin Schrödinger in 1926, in order to address the phenomenon of quantization in quantum mechanics as an eigenvalue problem.

The time-dependant Schrödinger equation.

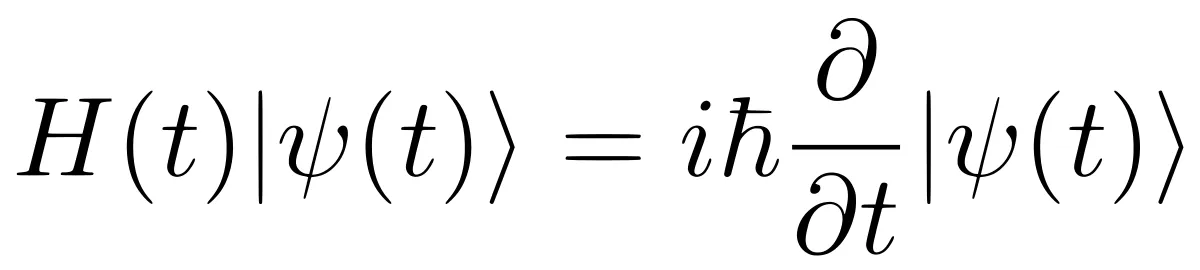
The Schrödinger equation is to Quantum Physics what Newton's 2^nd law of motion is to Classical Mechanics - it serves as a basis to predicting the future behaviour of a system as it evolves in time. This equation is used to obtain the allowed wavefunctions of a particle that is affected by a potential.

How does one go about using the equation to predict the future state of a quantum mechanical system? Here's the standard recipe that can be applied to solve most problems.

Find energy eigenvalues and eigenfunctions

Eigenvalues are the only possible outcomes of an energy measurement that is performed on the system. Whenever one of those energies is measured, the system collapses into the state described by the energy eigenfunction associated with that energy.

The time-independant form of the Schrödinger equation is used to determine eigenvalues and eigenfunctions. That form of the equation is the following:

$$H\psi_n=E_n\psi_n$$

Or writing out the formula for the Hamiltonian:

$$\left(-\frac{\hbar^2}{2m}\frac{\partial^2}{\partial x^2}+V\right)\psi_n=E_n\psi_n$$

Depending on the form of the potential V, finding the solutions of this equation will involve a more or less complicated differential equation!

Apply the normalization condition

A wavefunction is a statistical representation of a system - the square of the modulus of a wavefunction equates to a probability density function: $\left|\psi(x,t)\right|^2$ is a probability density function with respect to position, which, integrated between two boundaries, gives the probability to measure the particle in between those boundaries.

With that in mind, we can formulate the normalization condition:

$$\int_{-\infty}^{+\infty}\left|\psi(x,t)\right|^2dx=1$$

Which, in Dirac (or Bra-Ket) notation, is written more simply:

$$\langle\psi|\psi\rangle=1$$

This equation has an intuitive explanation: the particle must at any time be located somewhere in space.

The normalization condition is used to determine the normalization constant of any pure or superposition state of the system. Remembering to apply it is key, as a wavefunction only constitutes an accurate representation of a system once it has been normalized!

Combining energy eigenfunctions

Eigenfunctions can be combined together to form superposition states. These superposition states are important, as they also constitute valid solutions to the problem.

Superposition states are particularly interesting as, unlike pure states, their probability density functions evolve with time. You can explore the time-dependance of wavefunctions in this post.

And you can find out an example on how to apply the Schrödinger equation to solve a simple problem in this post.